PELUANG

Permutasi 

adalah susunan dari objek-objek atau unsur-unsur dengan memperhatikan urutan nya

Permutasi pengulangan

Jika urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali maka jumlah permutasinya adalah:

di mana n adalah banyaknya objek yang dapat dipilih dan r adalah jumlah yang harus dipilih.

Sebagai contoh, jika kamu memiliki huruf A, B, C, dan D dan kamu ingin mencari tahu ada berapa cara untuk menyusunnya dalam suatu grup yang berisi tiga angka maka kamu akan menemukan bahwa ada 4³ atau 64 cara untuk menyusunnya. Beberapa cara untuk menyusunnya adalah: AAA, BBB, CCC, DDD, ABB, CBB, DBB, dst.

Permutasi tanpa pengulangan

Jika urutan diperhatikan dan setiap objek yang tersedia hanya bisa dipilih atau dipakai sekali maka jumlah permutasi yang ada adalah:

di mana n adalah jumlah objek yang dapat kamu pilih, r adalah jumlah yang harus dipilih dan ! adalah simbol faktorial.

Sebagai contoh, ada sebuah pemungutan suara dalam suatu organisasi. Kandidat yang bisa dipilih ada lima orang. Yang mendapat suara terbanyak akan diangkat menjadi ketua organisasi tersebut. Yang mendapat suara kedua terbanyak akan diangkat menjadi wakil ketua. Dan yang mendapat suara ketiga terbanyak akan menjadi sekretaris. Ada berapa banyak hasil pemungutan suara yang mungkin terjadi? Dengan menggunakan rumus di atas maka ada 5!/(5-3)! = 60 permutasi.

Umpamakan jika n = r (yang menandakan bahwa jumlah objek yang bisa dipilih sama dengan jumlah yang harus dipilih) maka rumusnya menjadi:

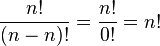 karena 0! = 1! = 1

Sebagai contoh, ada lima kotak kosong yang tersedia. Kelima kotak kosong itu harus diisi (tidak boleh ada yang kosong). Kelima kotak kosong itu hanya boleh diisi dengan angka 1,2,3,4,5. Ada berapa banyak cara untuk mengisi kotak kosong? Dengan menggunakan rumus n! maka ada 5! = 120 permutasi.

Permutasi Contoh :

  Dalam suatu kartu bridge, berapa cara untuk mengambil:

  a. Sebuah jantung atau sebuah daun

  b. Sebuah jantung atau kartu As

  c. Sebuah As atau King

  d. Sebuah kartu bernomor 2 hingga 10

JAWAB:

  a. Karena antar gambar kartu adalah saling   asing, maka banyak cara mendapatkan

  = 13 + 13 = 26 cara

  b. Banyak cara = 13+3 = 16 cara

  c. Banyak cara = 4+4 = 8 cara

  d. Banyak cara = 9+9+9+9 = 36 cara

Kombinasi

Adalah susunan dari objek-objek atau unsure-unsur dengan tidak memperhatikan urutan nya

Kombinasi tanpa pengulangan

Ketika urutan tidak diperhatikan akan tetapi setiap objek yang ada hanya bisa dipilih sekali maka jumlah kombinasi yang ada adalah:

Di mana n adalah jumlah objek yang bisa dipilih dan r adalah jumlah yang harus dipilih.

Sebagai contoh, kamu mempunyai 5 pensil warna dengan warna yang berbeda yaitu; merah, kuning, hijau, biru dan ungu. Kamu ingin membawanya ke sekolah. Tapi kamu hanya boleh membawa dua pensil warna. Ada berapa banyak cara untuk mengkombinasikan pensil warna yang ada? Dengan menggunakan rumus di atas maka ada 5!/(5-2)!(2)! = 10 kombinasi.

Kombinasi pengulangan

Jika urutan tidak diperhatikan dan objek bisa dipilih lebih dari sekali, maka jumlah kombinasi yang ada adalah:

Di mana n adalah jumlah objek yang bisa dipilih dan r adalah jumlah yang harus dipilih. Sebagai contoh jika kamu pergi ke sebuah toko donat. Toko donut itu menyediakan 10 jenis donat berbeda. Kamu ingin membeli tiga donat. Maka kombinasi yang dihasilkan adalah (10+3-1)!/3!(10-1)! = 220 kombinasi.

contoh 

Membeli selusin roti dari suatu toko roti yang menjual 8 jenis

roti, kemungkinannya adalah C ( 8+12-1 , 12 )

Bila diinginkan bahwa tiap jenis roti harus ada, kemungkinan

adalah C ( 12 + ( r – k ) – 1 , ( r- k ) ) =  C ( r-1 , k-1 )